分类

1. 稳定排序：插入排序、冒泡排序、归并排序、基数排序
2. 不稳定排序：选择排序、快速排序、希尔排序、堆排序

冒泡排序

算法思想

冒泡排序是一种简单的排序算法，通过循环遍历，将临近的两个元素进行比较，满足排序规则时，进行下一组元素对比；当不满足排序规则时，将两个元素交换位置，再继续进行下一组元素对比，确保最大的元素在一遍循环过后一定排在最后面；最后通过最多 $n^2$ 次循环对比，直到完全有序。

算法描述

1. 比较两个相邻的元素，如果第一个比第二个大，那么就交换他们的位置。
2. 重复步骤 $1$ 的操作，依次比较两两相邻的两个元素。所有元素对比过后表示一次循环结束。
3. 至多循环 $n-1$ 次，重复上面两个步骤。
4. 直到没有任何一组元素需要交换位置表示排序完成。

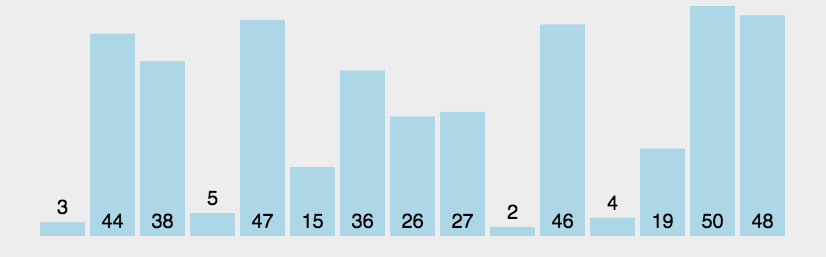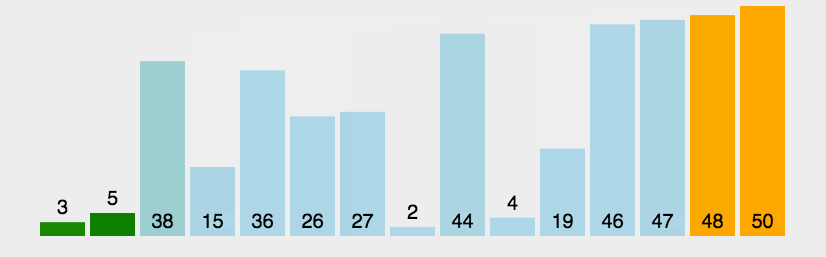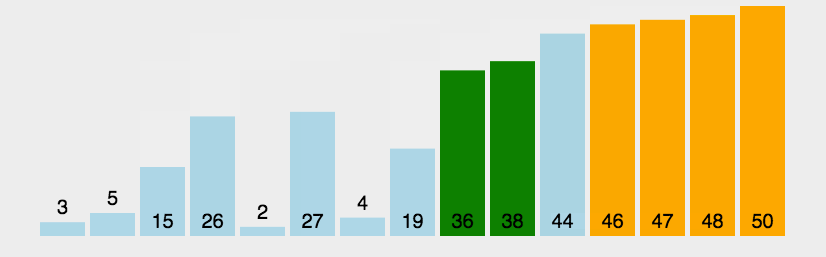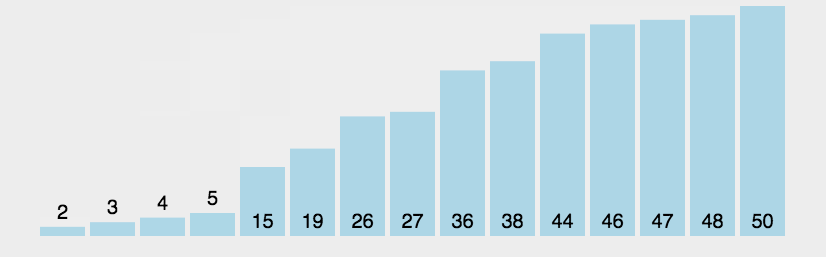
该算法可简单描述为：小泡上浮，大泡下沉

算法复杂度

1. 时间复杂度：$O(n^2)$
2. 空间复杂度：$O(1)$

算法实现

void Osort(int n,int*arr){
	int temp;
	for(int i=0;i<n-1;i++){
		for(int j=0;j<n-1-i;j++){
			if(arr[j+1]<arr[j]){
				temp=arr[j];
				arr[j]=arr[j+1];
				arr[j+1]=temp;
			}
		}
	}
}

插入排序

算法思想

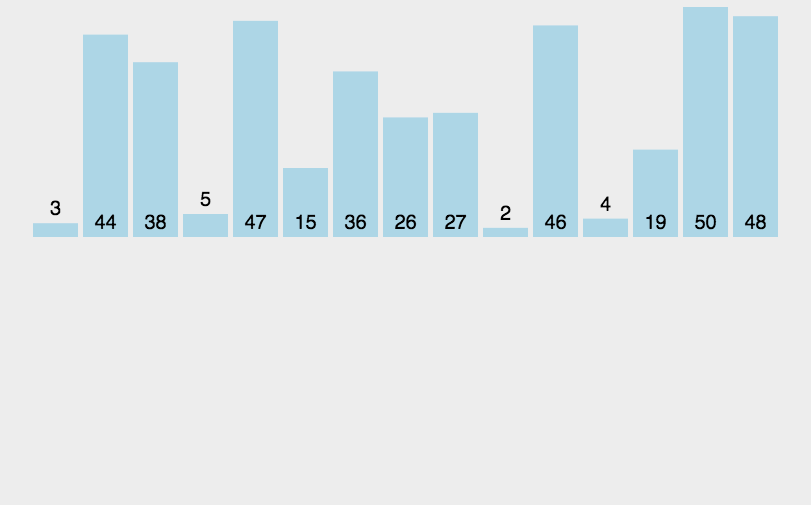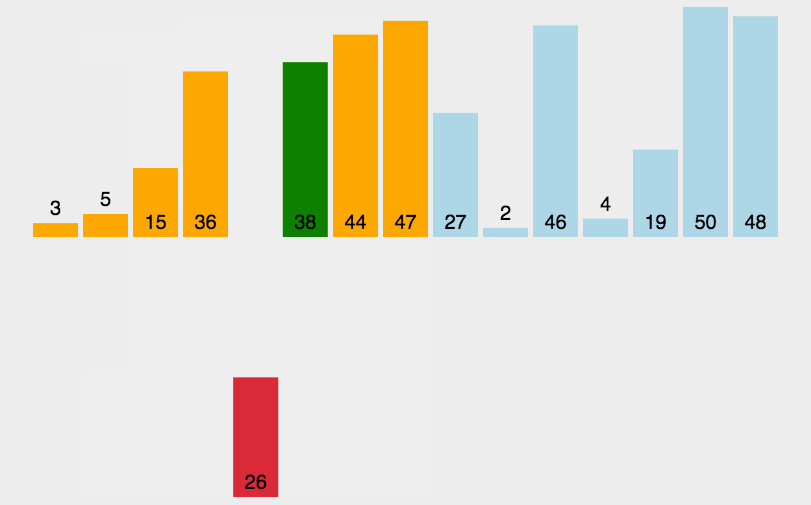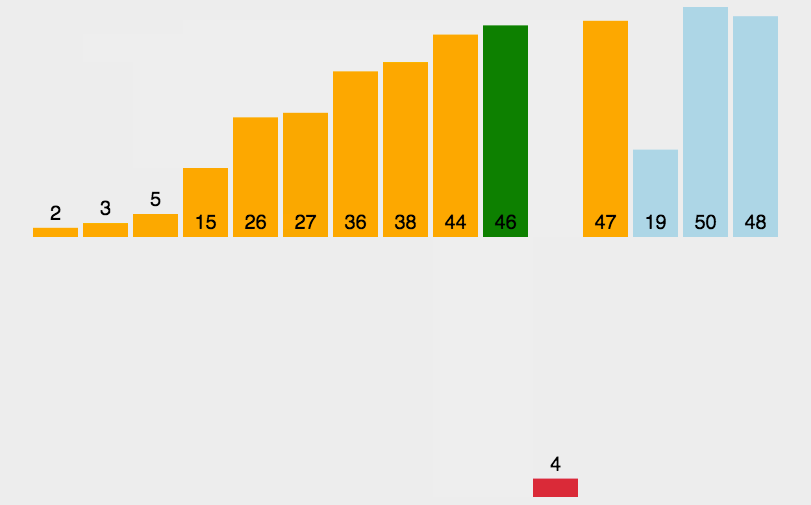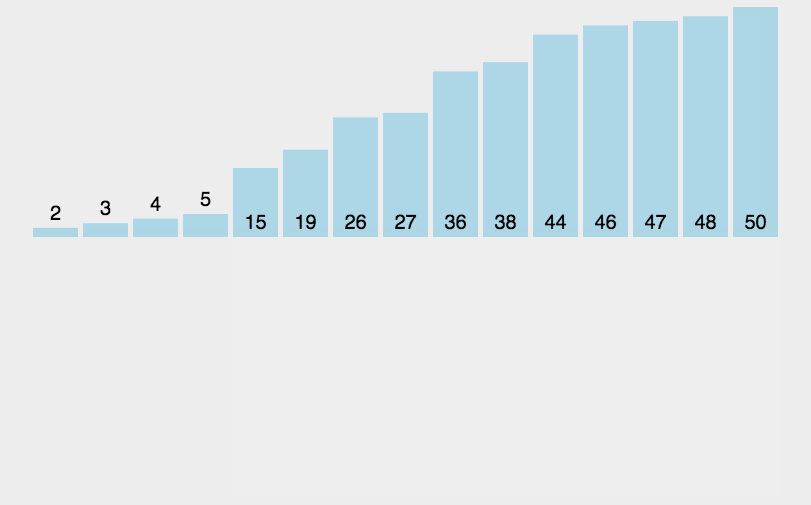
将列表中的每个元素依次和之前排好序的元素进行比较，找到合适的位置插入，使之前有序的列表保持依然有序。

算法描述

1. 从第 $2$ 个元素开始，选取第 $2$ 个元素 $i$ ，认为第 $1$ 个元素为一个只有一个元素的有序列表。
2. 将选取的元素与之前的元素依次比较，如果选取的元素小于于列表中的元素，交换他们的位置。
3. 选取下一个元素 $i+1$，重复步骤 $2$ ，直至列表中的每个元素都进行了步骤 $2$ 的操作。

算法复杂度

1. 时间复杂度：$O(n^2)$
2. 空间复杂度：$O(1)$

算法实现

void Isort(int n,int *arr){
	int temp;
	for(int i=1;i<n;i++){
		temp=arr[i];
		int j=0;
		for(j=i-1;j>=0;j--){
			if(temp<arr[j]){
				arr[j+1]=arr[j]; 
			}
			else
			break;
		}
		arr[j+1]=temp;
	}
}

选择排序

算法思想

从头开始，遍历列表找到最小值，把最小的值放在第一个位置，在遍历找到第二小的值放在第一个后面，以此类推，直到最后一个排好序。

算法描述

1. 遍历整个列表 $n$ 个元素，找到最小的元素，与第一个元素交换位置。
2. 遍历剩余的 $n-1$ 个元素，找到最小的元素，将它排在剩余 $n-1$ 个元素的第一个。
3. 以此类推，重复步骤 $2$ ，直到 $n-1$ 小于 $1$ 。

算法复杂度

1. 时间复杂度：$O(n^2)$
2. 空间复杂度：$O(1)$

算法实现

void Csort(int n,int *arr){
	int temp;
	for(int i=0;i<n-1;i++){
		for(int j=i+1;j<n;j++){
			if(arr[j]<arr[i]){
				temp=arr[j];
				arr[j]=arr[i];
				arr[i]=temp;
			}
		}
	}
}

快速排序（竞赛常用）

算法思想

快速排序采用分治的思想，首先将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

算法描述

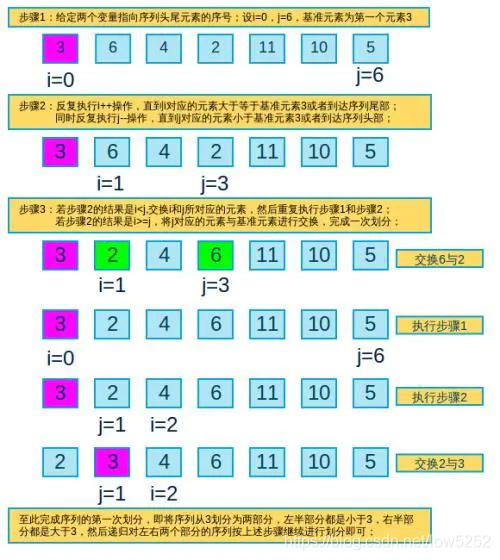
1. 选定一个基准元素
2. 从右往左找到比基准元素小的元素
3. 从左往右找到比基准元素大的元素
4. 交换左右找到的两个元素的位置
5. 重复上面 $2$ $3$ $4$ 步，直至左右两个元素相遇。

算法复杂度

时间复杂度：$O(nlogn)$

算法实现

void qsort(int l, int r, int* a){//递归处理左右两个子序列 
    if(l>=r) return; //边界条件，当 l>=r 时,不需要继续递归 
    if(r-l+1<=10){ //当子序列长度小于等于 10 时,使用插入排序处理 
        insert_sort(l,r,a);
        return;
    }
    int mid=a[(l+r)>>1]; // 中间值,使用位运算优化除法操作 
    int i=l-1, j=r+1;
    while(i<j) {
        do i++; while(a[i]<mid);
        do j--; while(a[j]>mid);
        if(i<j) swap(a[i],a[j]);
    }
    qsort(l,j,a);
    qsort(j+1,r,a);
}