旋转

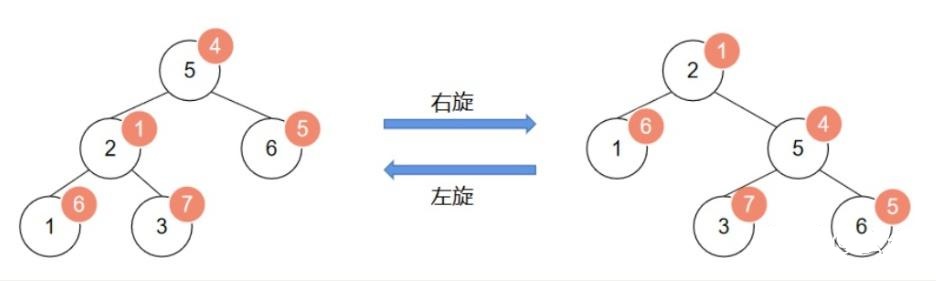
左旋：原根节点的右子节点变为新根节点，原根节点变为其右子节点的左子节点，并且其右子节点如果本就有左子节点，则该节点变为原根节点的右子节点。

右旋：原根节点的左子节点变为新根节点，原根节点变为其左子节点的右子节点，并且其左子节点如果本就有右子节点，则该节点变为原根节点的左子节点。

void rotate(Node *&o,int d){//d=0表示左旋转，d=1表示右旋，son[0]表示左儿子，son[1]表示右儿子
    Node* k=o->son[d^1]; //d^1与 1-d 等价，但速度更快
    o->son[d^1]=k->son[d]; 
    k->son[d]=o;
    o=k; //返回新根 
}

插入

每读入一个新节点，为它分配一个随机的优先级，插入到树中，在插入时动态调整树的结构，使它仍然是一棵Treap树。把新节点node插入到Treap树的过程有以下两步：

1. 用朴素的插入方法把node按键值大小插入到合适的子树上。
2. 给node随机分配一个优先级，如果node的优先级违反了堆的性质，即它的优先级比父节点高，那么就让node往上走，替代父节点，最后得到一个新的Treap树。

Treap树的删除

如果待删除的节点是叶子节点，直接删除。 如果待删除节点x有两个子节点，那么找到优先级最大的子节点，把x向相反的方向旋转，也就是把x向树的下层调整，直到x被旋转到叶子结点，然后直接删除。

权值越高，越靠上

#include<cstdio>
#include<iostream>
#include<ctime>//生成随机数 
using namespace std;

int id[5000005],n;
struct Node{
	int size;//以这个节点为根的子树的节点总数，用于名次树 
	int rank;//优先级，用于维持树的平衡性，优先级越高则节点在树的上层 
	int key;//键值，表示节点的值 
	Node *son[2];//son[0]表示左子树,son[1]表示右子树 
	//构造函数，用于初始化节点 
	Node(int size,int rank,int key):size(size),rank(rank),key(key){
		son[0]=son[1]=NULL;//一开始生成的左右子树都为空 
	}
	//重载小于运算符，用于比较节点的优先级 
	bool operator<(const Node &a) const{//"<"表示要重载的符号 
		return rank<a.rank;
	}
	//比较函数，用于判断插入节点的位置
	int cmp(int x) const{
		if(x==key) return -1;//返回 -1表示键值相等 
		return x<key?0:1;//返回 0表示插入到左子树，返回 1表示插入右子树  
	} 
	//更新节点的 size属性，表示该节点为根的子树的节点总数 
	void updata(){
		size=1;
		if(son[0]!=NULL) size+=son[0]->size;
		if(son[1]!=NULL) size+=son[1]->size;
	}
};
//旋转 d=0表示左旋转,d=1表示右旋,son[0]表示左儿子，son[1]表示右儿子
void rotate(Node *&o,int d){
    Node *k=o->son[d^1]; //记录当前节点的另一个子树,d^1与 1-d 等价，但速度更快
    o->son[d^1]=k->son[d];//将当前节点的另一个子树的相应子树更新为 k的相应子树 
    k->son[d]=o;//将当前节点连接到 k的相应子树上
	o->updata();//更新当前节点的 size属性 
    k->updata();//更新当前节点的 size属性 
	o=k;//更新当前节点为 k节点，实现旋转操作 
}
//把 x插入到树中 
void insert(Node *&o,int x){
	if(o==NULL) o=new Node(1,rand(),x);//如果节点为空，创建键值为 x,优先级为随机数的节点 
	else{
		int d=o->cmp(x);//比较当前节点的键值和要插入节点的键值 x,-1表示相等,0表示大于 x,1表示小于 x 
		insert(o->son[d],x);//递归插入节点到当前节点的左子树或右子树  
		o->updata();//更新当前节点的 size
		if(o<o->son[d])//如果当前节点的优先级小于它的子节点的优先级
			rotate(o,d^1);//旋转，维持树的平衡性  
	}
}
//返回第 k大的数 
int kth(Node *o,int k){
	//如果当前节点为空，或者 k小于等于 0,或者 k大于当前节点子树的节点数，返回 -1 
	if(o==NULL||k<=0||k>o->size) return -1;
	//用于计算当前节点的右子树的节点数量 
	int s=o->son[1]==NULL?0:o->son[1]->size;
	if(k==s+1) return o->key;//如果 k等于当前节点右子树节点数量 +1,表示当前节点就为第 k大的数 
	else if(k<=s) return kth(o->son[1],k);//如果 k小于等于当前子节点的右子树节点数量，递归在右子树中找第 k大的数
	else return kth(o->son[0],k-s-1);//如果 k大于当前子节点的左子树节点数量，递归在左子树中找第 k大的数 
} 
//返回元素 k的名次 
int find(Node *&o,int k){
	if(o==NULL) return -1;
	int d=o->cmp(k);//比较当前节点的键值和目标值 x,-1表示相等,0表示当前节点大于 k,1表示当前节点小于 k 
	if(d==-1)
		return o->son[1]==NULL?1:o->son[1]->size+1;
	else if(d==1)
		return find(o->son[1],k);
	else{
		int temp=find(o->son[0],k);
		if(temp==-1) return -1;
		else return o->son[1]==NULL?temp+1:temp+1+o->son[1]->size;
	} 
} 
int main(void){
	while(~scanf("%d",&n)&&n!=0){
		//使用当前时间作为随机数种子，让每次程序运行时的随机数序列不同  
		srand(time(NULL));
		int k,g;
		scanf("%d %d",&k,&g);//老和尚的数据 
		Node *root=new Node(1,rand(),g);//创建根节点,键值为 g,优先级是随机数 
		id[g]=k;//将节点的编号与名次存入 id数组中
		printf("%d %d\n",k,1);
		for(int i=2;i<=n;i++){
			scanf("%d %d",&k,&g);//入列 
			id[g]=k;
			insert(root,g);//插入节点到名次树中
			int t=find(root,g);//返回新插入节点的名次 
			int ans1,ans2,ans;
			ans1=kth(root,t-1);//找前一位老和尚 
			ans2=kth(root,t+1);//找后一位老和尚 
			if(ans1!=-1&&ans2!=-1)
				ans=ans1-g>=g-ans2?ans2:ans1;//判断前一名和后一名中与当前节点距离更近的节点 
			else if(ans1==-1) ans=ans2;
			else ans=ans1;
			printf("%d %d\n",k,id[ans]);//输出编号和名次 
		}
	} 
	return 0;
}